Физика: Движение
Написах този урок в началото на 2010-та с идеята да направя серия от уроци по физика. В крайна сметка времето намаля малко след това (а и мотивацията ми също :) ). Това е (за сега) единствения урок.
Започваме с краткия курс по физика. В него ще се запознаем с някои основни понятия от физиката и механиката на непрекъснатите среди. Допускам че всички читатели имат елементарна идея от анализ и няма да се впускам в подробности за производните и интегралите. Все пак ще се старая да давам допълнителни линкове, където ми се види, че математиката изисква малко повече четене.
Уроците са доста дългички и няма да задръствам заглавната страница с тях. Та, приятна занимавка и…
Кинематика
Изучаването на различните видове движение от чисто геометрична гледна точка се нарича Кинематика. Обикновено движението е следствие на някакви сили които влияят на тялото. Ако вземем и тях предвид, ще стигнем до дела от механиката, който се нарича Динамика. С него ще се занимаваме в друг урок.
Нека разгледаме понятието „Движение” и неговите характеристики. В този уводен урок ще вземем предвид тези ограничения за движението.
- То ще е винаги по права линия.
- Няма да взимаме предвид всичките сили, които го причиняват и му влияят.
- Обектите, които се движат са монолитни1
Позиция и скорост
Тъй като разглеждаме движението на обект по една линия, достатъчно ни е едно число, за да опишем позицията на обекта. Ако той се придвижи от х1 до х2, имаме преместване на позицията му (спомнете си, че преместването (разликата) се бележи с гръцката буква Δ (главно делта)). Това преместване бележим с
\[\Delta x = x_{2} - x_{1} \quad (1)\]Например ако обект се придвижи от позиция 5 до позиция 8, имаме Δx = 8 – 5 = 3. Ако обект се предвижи от позиция 10 до позиция 6, ще имаме Δx = 6 – 10 = -4 и т.н. Виждаме че отместването е векторна величина. Сиреч такава, която има и посока, и магнитуд2.
Отместването на един обект се извършва за някакво количество време. Подобно на позицията в пространството, можем да отбележим и позиция във времето. Ще казваме, че преместването във времето от момент t1 до момент t2 е Δt = t2 – t1. Точно както и за позицията.
Скоростта на един обект не е нищо друго, а отношението на изминатото разстояние (преместване в позицията) отнесено към изминалото време, или
\[v = \frac{\Delta x}{\Delta t} = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} \quad (2)\]Следват две графики, които са удобни за разглеждане на скоростта. Наричат се графики разстояние-време и показват отношението между двете.
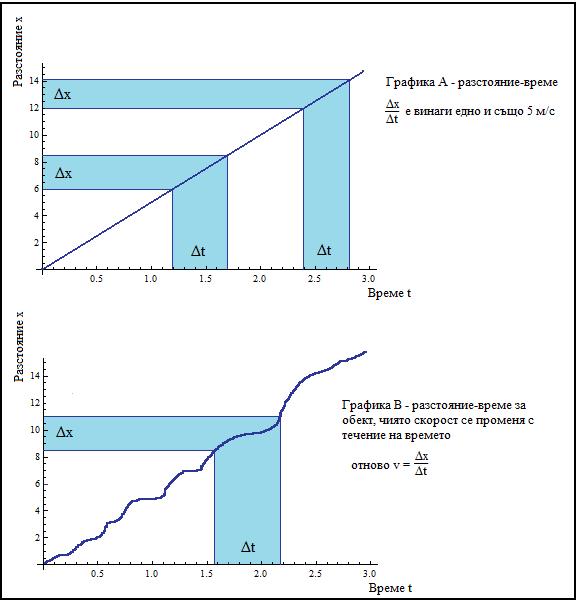
Oт графика В се вижда, че горната формула ни дава средна скорост, а не текуща. Текущата скорост се мени непрекъсано, но избирайки два момента от време и виждайки какво разстояние е изминато между тях (или обратното), можем да намерим средната скорост на обекта за даденото време или разстояние. Все пак, по-често, когато задаваме въпроса „Колко бързо?” имаме предвид именно текущата скорост на обекта. (От сега нататък, ще казваме само „скорост”, когато имаме предвид текуща скорост, а когато имаме предвид средна скорост, специално ще казваме „средна”).
Скоростта в определен момент от времето се изчислява именно като специфицираме този момент. За да получим момент, трябва просто безкрайно да намалим интервала от време, който взимаме предвид в горната формула. Това се получава, като намерим нейната граница, когато Δt клони към нула.
Сега, от една страна можем да видим, че средната скорост представлява наклона, или тангентата, на функцията на пътя в горните графики и да обърнем внимание, че горното разсъждение ни води до тангента в точка. От друга страна, можем просто да си спомним дефиницията за производна3. Всяко от двете наблюдения ни показва, че моментната скорост е именно частната производна на х по t. Или:
\[v = \lim_{\Delta t \rightarrow 0}\frac{\Delta x}{\Delta t} = \frac{dx}{dt} \quad (3)\]Ускорение
Когато скоростта на едно тяло се измени, то претърпява ускорение. Например, ако в един момент се движим с 6 м/с, а една секунда по-късно с 8 м/с, значи скоростта ни се е увеличила с 2 метра в секунда за една секунда. Така получихме и мерна единица за ускорение: метър в секунда в секунда или за по-кратко метър в секунда на квадрат. Това се бележи с m/s2, а понякога и ms-2. Естествено и всяка друга комбинация от разстояние върху време по време е подходяща (например миля в минута в час). Често използвана единица за ускорение е и g. С него се бележи ускорението на падащ обект върху земната повърхност4 (игнорирайки съпротивлението на въздуха). Земното ускорение g е равно на 9.807 m/s2.
Вижда се, че както скоростта е отношение на разстояние към време, то така и ускорението е отношение на скорост към време. И по същия начин, както говорихме за средна и текуща скорост скорост, така можем да говорим за средно ускорение:
\[a_{avg} = \frac{v_{2} - v_{1}}{t_{2} - t_{1}} = \frac{\Delta v}{\Delta t} \quad (4)\]…и за текущо (моментно) ускорение:
\[a = \lim_{\Delta t \rightarrow 0}\frac{\Delta v}{\Delta t} = \frac{dv}{dt} \quad (5)\]Сега, прилагайки формула 3, виждаме следното:
\[a = \frac{dv}{dt} = \frac{d}{dt} \frac{dx}{dt} = \frac{d^{2}x}{dt^{2}} \quad (6)\]Казано с думи: моментното ускорение е втората производна на функцията за движение х по променливата за време t. И също така, ако разгледаме горната графика и в нея сменим думата „разстояние” със „скорост”, ще получим именно графики скорост-време, които илюстрират ускорението.
Константно ускорение
Много често се случва ускорението да е константно. Това означава, че скоростта ще се мени линейно (или ще остане константа, ако ускорението е 0). Нека се спрем за малко на този случай. Когато една функция е линейна, средната и стойност съвпада със самата функция (както се вижда на графика А). Това значи че в този случай:
\[a = a_{avg} = \frac{v-v_{0}}{t-0} \quad (7)\]Нека леко променим нотацията, използвайки t за общото време и v за скоростта в този момент, а v0 за скоростта във началния момент 0. Тогава горната формула 7 може да бъде наредена и така:
\[v = v_{0} + at \quad (8)\](или скоростта е равна на началната скорост плюс ускорението, умножено по времето)
Като имаме предвид промените в нотацията, които направихме, можем да сведем формула 2 до:
\[x = x_{0} - v_{avg}t \quad (9)\](Тук явно използваме средна скорост, защото, естествено, това че ускорението е константа, не значи, че и скоростта ще е такава). Продължавайки нататък, взимаме предвид, че имаме константно ускорение. Следователно средната скорост е половината от разликата на крайната и началната. Замествайки този начин да получим средната скорост във формула 8, получаваме:
\[v_{avg} = v_{0} + \frac{1}{2}at \quad (10)\]И накрая, замествайки 10 в 9, получаваме:
\[x - x_{0} = v_{0}t + \frac{1}{2}at^{2} \quad (11)\](изминатият път е равен на началната скорост по времето плюс половината от ускорението по времето на квадрат)
Запомнете формули 8 и 11. Те се наричат основни уравнения за кинематика с константно ускорение и с тях би трябвало да може да се реши всяка задача на тази тема. Например ако искаме да проверим нещо, което всички сме учили във втори клас и се опитаме да елиминираме ускорението „а“ от двете (изразяваме го чрез останалите променливи във формула 8 и заместваме в 11), ще получим:
\[x - x_{0} = \frac{1}{2}(v_{0} + v)t \quad (12)\]Виж ти. Излиза, че изминатото разстояние е равно на средната скорост умножена по времето, без значение какво е ускорението. Кой би помислил така?…
Видяхме че можем да изведем основните уравнения за кинематика с константно ускорение чрез аритметика. Ето и един алтернативен метод.
Използвайки формула 6, виждаме, че можем да напишем неопределен интеграл от двете страни. Знаем че „а“ е константа, следователно можем да я изкараме без проблеми пред знака за интеграл и да получим това:
\[dv = a\ dt \Leftrightarrow \int dv = \int a\ dt \Leftrightarrow \int dv = a\int dt \Leftrightarrow v = at + C \quad (13)\]Крайната скорост е равна на ускорението по времето плюс константа. За да изчислим константата, нека сложим времето да е 0. Тогава скоростта е v0. Следователно констатата е равна на v0. Така получаваме формула 8.
Използвайки формула 3, отново можем да напишем интеграл от двете страни, после прилагайки формула 8 и използвайки че v0 и a са константи можем да разделим интеграла. От там следва:
\[dx = v\ dt \Leftrightarrow \int dx = \int v\ dt \Leftrightarrow^8 \int dx = \int (v_{0} + at)dt\Leftrightarrow\\ \Leftrightarrow\int dx = v_{0}\int dt + a\int t\ dt \Leftrightarrow x = v_{0}t + \frac{1}{2}at^{2}+C \quad (14)\]Накрая, за да намерим константата, заместваме времето с 0, където пътят е x0 и получаваме точно формула 11.
Не-константно ускорение
Въпреки, че в преобладаващото мнозинство от случаите ускорението е константно (или толкова близко до константно, че приближението е абсолютно приемливо5), понякога това не е така. Както може би се досещате, аритметиката няма как да ни помогне в този случай.
След като ускорението се дефинира чрез скорост a = dv/dt пряко следствие на Фундаменталната теорема на анализа6 е:
\[v_{1} - v_{0} = \int_{t_{0}}^{t_{1}}a\ dt \quad (15)\]Тоест, промяната на скоростта между моментите от време t0 и t1 е лицето на графиката на ускорението между същите две точки. Което е по-интересно е, че ако имаме функция за скорост, можем да намерим изминатото разстояние по идентичен начин.
\[x_{1} - x_{0} = \int_{t_{0}}^{t_{1}}v\ dt \quad (16)\]Ето и един кратък пример. Да допуснем че имаме равномерно ускорение, последвано от временно константо ускорение и след това забавяне (отрицателно ускорение). Ускорението дефинираме така:
\[a(x) = \begin{cases} 3x, & \mbox{if }x < 5 \\ 15, & \mbox{if }x < 8 \\ 47 - 4x, & \mbox{if }x \geq 8 \\ \end{cases}\]Тогава скоростта v в определен момент t ще е:
\[v = \int_{0}^{t}a(x)\ dx\]А изминатото разстояние в този момент ще е:
\[x = \int_{0}^{t}\left (\int_{0}^{t'}a(x)\ dx \right )dt'\]Съответно в секунда 4 ще се движим с ускорение 12m/s2, скорост 24 m/s и ще сме изминали разстояние 32 метра. Ето и графика за примера:
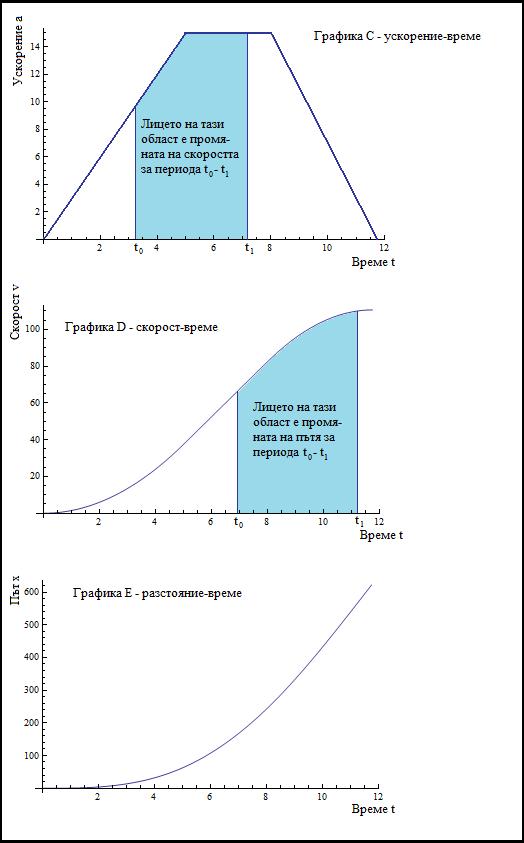
Задачки
Ето няколко примерни задачки по темата, с които можете да се упражните:
- Момче търкулва гума по хълм. Гумата се търкаля с 3 m/s2. Какво разстояние ще измине гумата за 8 секунди?
- Същото момче се опитва да бяга наравно с гумата. Неговата максимална скорост е 4.5 m/s. Какво разстояние ще измине, докато спре да може да поддържа темпото на гумата?
- Велосипедист се спуска по хълм с постоянно ускорение 2.5 m/s2. Колко време ще отнеме на велосипедиста да стигне от скорост 5 m/s до 20 m/s
- Защо, когато баскетболист скача за да хване висока топка, съществува илюзията че той „виси“ във въздуха? (Вземете предвид ускорението g на Земята)
Следващият урок
В следващия урок ще разгледаме по-сложно движение на обекти – в две и повече измерения – и математиката асоциирана с него. Ще се спрем и на начини за решаване на интегралите за скоростта и пътя чрез числени методи.
Бележки
-
Монолитни значи идеалния вариант, в който всяка тяхна част се движи абсолютно едновременно с останалите. В общия случай това не е така. Ако вие ходите, първо се придвижва кракът ви, после торсът и т.н. ↩
-
Когато говорим за едно измерение, посоката е знакът + или -, а магнитуд е разстоянието между двете точки. Можете да си представите едноизмерен вектор. Имаме посока, имаме и абсолютна стойнсот (или модул). ↩
-
За дефиницията на производна можете да видите страницата във Уикипедия ↩
-
Да, ускорението е абсолютно достатъчно, за да покажем как един обект ще пада върху земната повърхност, ако игнорираме съпротивлението на въздуха. Точно това пръв казва Галигей, а космонавтите от „Аполо 15“ показват, като пускат в свободно падане перо и чук и те едновременно падат на лунната повърхност (клипче). Именно заради съпротивлението на въздуха това не е интуитивно за човек и той подсъзнателно очаква, че по-тежкия предмет ще пада по-бързо. ↩
-
Специално за игри и компютърни симулации, често, даже и да можем да съставим пълно решение на конкретна задача, съзнателно избираме задоволително приближение, за да имаме по-прости изчисления. Тук конкретно, винаги предпочитаме да изберем простите аритметични решения, ако можем, вместо да се борим с интегрирането. ↩
-
Фундаменталната теорема на анализа е изказана във Уикипедия ↩